Introduction to C Programming
Looping Constructs

Computers are very good at performing repetitive tasks very quickly. In this section we will learn how to make computer repeat actions either a specified number of times or until some stopping condition is met.

while Loops ( Condition-Controlled Loops )

Both while loops and do-while loops ( see below ) are condition-controlled, meaning that they continue to loop until some condition is met.
Both while and do-while loops alternate between performing actions and testing for the stopping condition.
While loops check for the stopping condition first, and may not execute the body of the loop at all if the condition is initially false.
Syntax:

while( condition ) body;

where the body can be either a single statement or a block of statements within < curly braces >.

Example:

int i = 0; while( i < 5 ) printf( "i = %d\n", i++ ); printf( "After loop, i = %d\n", i );

do-while Loops

do-while loops are exactly like while loops, except that the test is performed at the end of the loop rather than the beginning.
This guarantees that the loop will be performed at least once, which is useful for checking user input among other things ( see example below. )
Syntax:

do < body; >while( condition );

In theory the body can be either a single statement or a block of statements within < curly braces >, but in practice the curly braces are almost always used with do-whiles.
Example:

int month; do < printf( "Please enter the month of your birth >" ); scanf( "%d", &month ); > while ( month < 1 || month >12 );

Note that the above example could be improved by reporting to the user what the problem is if month is not in the range 1 to 12, and that it could also be done using a while loop if month were initialized to a value that ensures entering the loop.
The following diagram shows the difference between while and do-while loops. Note that once you enter the loop, the operation is identical from that point forward:

for Loops

for-loops are counter-controlled, meaning that they are normally used whenever the number of iterations is known in advance.
Syntax:

where again the body can be either a single statement or a block of statements within < curly braces >.

Details:

The initialization step occurs one time only, before the loop begins.

The condition is tested at the beginning of each iteration of the loop.

If the condition is true ( non-zero ), then the body of the loop is executed next.
If the condition is false ( zero ), then the body is not executed, and execution continues with the code following the loop.

Special Notes:

The third part of the loop is labeled "incrementation", because it usually takes the form of "i++" or something similar. However it can be any legal C/C++ statement, such as "N += 3" or "counter = base + delta".
In the example above, the variable i is declared before the loop, and continues to exist after the loop has completed. You will also see occasions where the loop variable is declared as part of the for loop, ( in C99 ), in which case the variable exists only within the body of the loop, and is no longer valid when the loop completes:

for( int i = 0; i < 5; i++ ) printf( "i = %d\n", i ); printf( "After loop, i is no longer valid\n" );

( In Dev C++ you can specify support for C99 by selecting Project->Project Options from the menu, and then selecting the Parameters tab. Under "C compiler", add the line: -std=c99 )

The comma operator

C has a comma operator, that basically combines two statements so that they can be considered as a single statement.
About the only place this is ever used is in for loops, to either provide multiple initializations or to allow for multiple incrementations.
For example:

int i, j = 10, sum; for( i = 0, sum = 0; i < 5; i++, j-- ) sum += i * j;

break and continue

break and continue are two C/C++ statements that allow us to further control flow within and out of loops.
break causes execution to immediately jump out of the current loop, and proceed with the code following the loop.

continue causes the remainder of the current iteration of the loop to be skipped, and for execution to recommence with the next iteration.

In the case of for loops, the incrementation step will be executed next, followed by the condition test to start the next loop iteration.
In the case of whileanddo-while loops, execution jumps to the next loop condition test.

Infinite Loops

Infinite loops are loops that repeat forever without stopping.
Usually they are caused by some sort of error, such as the following example in which the wrong variable is incremented:

int i, j; for( i = 0; i < 5; j++ ) printf( "i = %d\n", i ); printf( "This line will never execute\n" );

Other times infinite loops serve a useful purpose, such as this alternate means of checking user input:

while( true ) < printf( "Please enter a month from 1 to 12 >" ); scanf( "%d", &month ); if( month > 0 && month

Empty Loops

A common error is to place an extra semi-colon at the end of the while or for statement, producing an empty loop body between the closing parenthesis and the semi-colon, such as:

int i; for( i = 0; i < 5; i++ ); // Error on this line causes empty loop printf( "i = %d\n", i ); // This line is AFTER the loop, not inside it.

int i = 0; while( i < 5 ); // Error - empty loop on this line printf( "i = %d\n", i++ ); // Again, this line is AFTER the loop.

In the case of the while loop shown above, it is not only empty but also infinite.
There are some very rare circumstances in which a programmer will deliberately write an empty loop, most of which are beyond the scope of this course. ( This is know as a busy loop. )
In this case, the semicolon should be placed on a line by itself, and clearly commented to indicate that the empty loop is deliberate and not an oversight:

while( ( error = someFunction( ) ) != 0 ) ; // Empty loop - Does nothing forever, until someFunction returns a zero printf( "error = %d\n", error ); // After the loop. error must be zero to get here.

Nested Loops

The code inside a loop can be any valid C code, including other loops.
Any kind of loop can be nested inside of any other kind of loop.
for loops are frequently nested inside of other for loops, for example to produce a simple multiplication table:

const int NROWS = 10; const int NCOLS = 10; for( int r = 0; r < NROWS; r++ ) < // Loop through rows for( int c = 0; c < NCOLS; c++ ) < // Loop through columns printf( "%5d", r * c ); // No newline in the middle of a row >// End of loop through columns printf( "\n" ); // One newline at the end of each row > // End of loop through rows

Some programmers like to use successive integers i, j, k, l, etc. for use in nested for loops. This can be appropriate if the mathematics being implemented uses multiple ijk subscripts.

Other times it can be less confusing to use alternative variables that are more meaningful to the problem at hand, such as the r and c variables used above to keep track of rows and columns.

Floating Point Increments Within Loops

Engineers and scientists frequently write iterative programs in which a floating point value steps through a range of values in small increments.
For example, suppose the "time" variable needs to change from a low of tMin to a high of tMax in steps of deltaT, where all these variables are doubles.
The obvious BUT INCORRECT approach is as follows:

for( time = tMin; time 

  So why is this so wrong? 
  If deltaT is small and/or the range is large ( or both ), the loop may execute for thousands of iterations.
  That means that by the end of the loop, time has been calculated by the summation of thousands of addition operations.
  Numbers that seem "exact" to us in decimal form, such as 0.01 are not exact when the computer stores them in binary, which means that the value used for deltaT is really an approximation to the exact value.
  Therefore each addition step introduces a very small amount of roundoff error, and by the time you add up thousands of these errors, the total error can be significant.

int nTimes = ( tMax - tMin ) / deltaT + 1; for( int i = 0; i < nTimes; i++ ) < time = tMin + i * deltaT; // NOW use a more accurate time variable

  Or alternatively if you know the minimum, maximum, and number of desired iterations:

double deltaT = ( tMax - tMin ) / ( nTimes - 1 ); for( int i = 0; i < nTimes; i++ ) < time = tMin + i * deltaT; // NOW use a more accurate time variable

  In general there are four values that can be used to specify stepping through a range - the low end of the range, the high end of the range, the number of step to take, and the increment to take on each step - and if you know any three of them, then you can calculate the fourth one. 
  The correct loop should use an integer counter to complete the loop a given number of times, and use the low end of the range and the increment as shown to calculate the floating point loop variable at the beginning of each iteration of the loop.

  The number of times that the loop executes is now controlled by an integer, which does not have any roundoff error upon incrementation, so there is no chance of performing one too many or one too few iterations due to accumulated roundoff.
  The time variable is now calculated from a single multiplication and a single addition, which can still introduce some roundoff error, but far less than thousands of additions.

  The +1 is needed in order to include both endpoints of the range.
  Suppose tMax were 20 and tMin were 10, and deltaT were 2. 
  The desired times would be 10, 12, 14, 16, 18, 20, which is a total of 6 time values, not 5. ( Five intervals if you want to look at it that way. )
  ( 20 - 10 ) / 2 yields 5, so you have to add the extra 1 to get the correct number of times of 6.

  Constant - Take the average of the inputs at the end points, evaluate f( average input ), and assume the function is constant over the range.
  Linear - Evaluate the function at the endpoints, and then use a linear interpolation of the endpoint function values in between.
  Non-Linear - Linearly interpolate the function inputs over the range, and at each evaulation point, evaluate the function of the interpolated inputs.

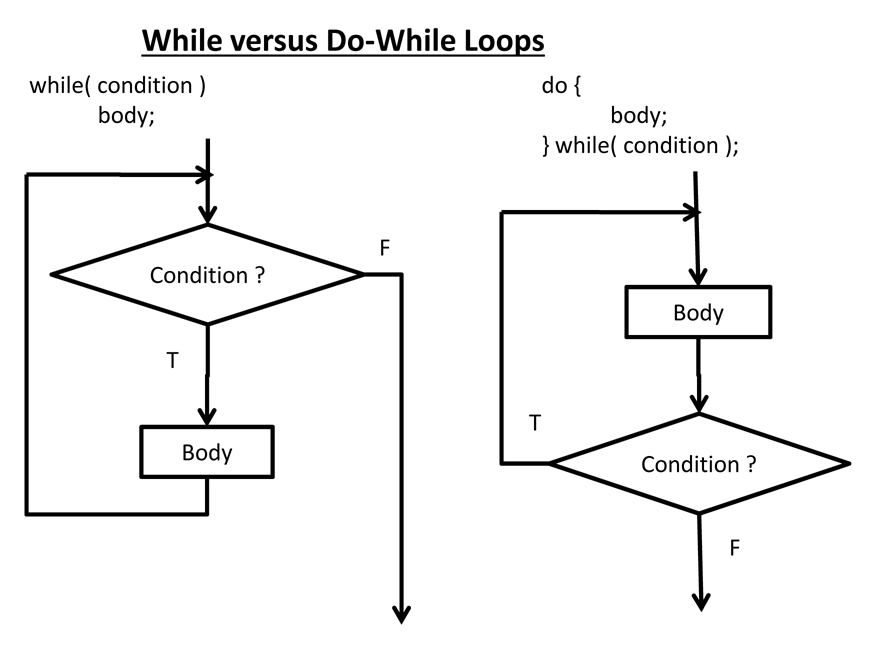
When to Use Which Loop ?

  If you know ( or can calculate ) how many iterations you need, then use a counter-controlled ( for ) loop.
  Otherwise, if it is important that the loop complete at least once before checking for the stopping condition, 
or if it is not possible or meaningful to check the stopping condition before the loop has executed at least once, 
then use a do-while loop.
  Otherwise use a while loop.

Exercises

  Write a program that generates a table showing the difference between "time1" calculated as "time1 += deltaT" and "time2" calculated as "time2 = i * deltaT", for iterations from 0 up to an upper limit specified by the user. The user should also specify a frequency for how frequently (s)he wants the results printed in the table. So if they enter 10 for the frequency you should print results every 10th time through the loop, and if they enter 100, then print every 100th time through the loop, etc. Hint: Use mod for the printing frequency.
  Write a program to calculate epsilon, the smallest value that can be added to 1.0 and still be distinguished from 1.0. Hint: Start with epsilon equal to 1.0, and then keep dividing it by 2.0 until 1.0 + epsilon / 2.0 is indistinguishable from 1.0;

Introduction to C Programming Looping Constructs